CHANGING THE BASE OF A LOGARITHM

Let a, b, and x be positive real numbers such that and (remember x must be greater than 0). Then can be converted to the base b by the formula

Let's verify this with a few examples.

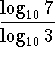Example 1: Find to an accuracy of six decimals. Note that the answer will be between 1 and 2 because and , and 7 is between 3 and 9. According to the change of logarithm rule, can be written tex2html_wrap_inline134 .

When the base is 10, we can leave off the 10 in the notation. Therefore 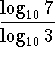tex2html_wrap_inline134 can be written . Using your calculator,

You will note that the answer is between 1 and 2.

Let's check the answer. If , our answer is correct. . Close enough. Why isn't it 7 exactly? Well we rounded to six places, so our answer won't check exactly. If we rounded to ten places, then when we checked the answer, it would be closer to 7 than this answer.

Example 2: We could work the same problem by converting to the base e. According to the change of logarithm rule, can be written . When the base is e, we can leave off the e in the notation and can be written . Using your calculator,

You will note that the answer is between 1 and 2.

Example 3: Find . We know that and , and that 18 is between 16 and 32; therefore, we know that the exponent we are looking for is between 4 and 5. In fact, it is closer to 4 than to 5 because 18 is closer to 16 than it is to 32.

Let's solve this problem by changing the base to 10. can be written tex2html_wrap_inline166 . Using your calculator,

Let's check the answer. If , our answer is correct. . Close enough. Why isn't it 18 exactly? Since we rounded tex2html_wrap_inline166 to six places, our answer won't check exactly. If we rounded to ten places, then when we checked the answer, it would be closer to 18 than this answer.

Example 4: We could work the problem in Example 3 by converting to the base e. According to the logarithmic rule, can be written . Using your calculator,

The answer is the same as the answer you found when you converted the base to 10.

If you would like to review more examples of changing the base of a logarithm, click on Example.

Work the following problems and click on answer if you want to check your answer and review the solution.

Problem 1: Find .

Answer.

Problem 2: Find .

Answer.

Problem 3: Find .

Answer.

Problem 4: Convert to the base 2.

Answer.

[Menu Back to Exponential Functions]

[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus