 GRAPHS OF EXPONENTIAL FUNCTIONS
GRAPHS OF EXPONENTIAL FUNCTIONS  GRAPHS OF EXPONENTIAL FUNCTIONS
GRAPHS OF EXPONENTIAL FUNCTIONS 
GRAPHS OF EXPONENTIAL FUNCTIONS
By Nancy Marcus
In this section we will illustrate, interpret, and discuss the graphs of exponential functions. We will also illustrate how you can use graphs to HELP you solve exponential problems and check your answers.
Reflection across the x-axis: The graph of f(x) versus the graph of -f(x).
Example 1: Graph the function
![]() and graph the function
and graph the function
![]() on
the same rectangular coordinate system. Answer the following
questions about each graph:
1.In what quadrants is the graph of the function
on
the same rectangular coordinate system. Answer the following
questions about each graph:
1.In what quadrants is the graph of the function ![]() located?
located?
2.In what quadrants is the graph of the function ![]() located?
located?
3.What is the x-intercept and the y-intercept of the graph of
the function ![]() ?
?
4.What is the x-intercept and the y-intercept of the graph of
the function ![]() ?
?
5.Find the point (2, f(2)) on the graph of ![]() and
find (2, g(2)) on the graph of
and
find (2, g(2)) on the graph of ![]() .
.
6.What do these two points have in common?
7.Describe the relationship between the two graphs.
8.How would you physically move the graph of ![]() so that it is superimposed on the graph of
so that it is superimposed on the graph of ![]() ? Where
would the point (0, 1) on
? Where
would the point (0, 1) on ![]() be located after such a move?
be located after such a move?
9.What do the two equations have in common?
|
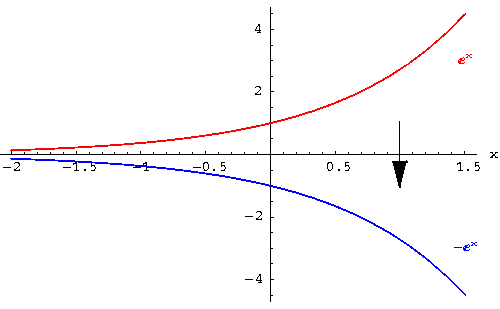
1.You can see that the graph of the function ![]() is located
in quadrants I and II above the x-axis.
is located
in quadrants I and II above the x-axis.
2.You can see that the graph of the function ![]() is located in quadrants III and IV below the x-axis.
is located in quadrants III and IV below the x-axis.
3.Note that the graph of ![]() does not cross the
x-axis anywhere, and crosses the y-axis at 1.
does not cross the
x-axis anywhere, and crosses the y-axis at 1.
4.Note that the graph of ![]() does not cross the
x-axis anywhere, and crosses the y-axis at - 1.
does not cross the
x-axis anywhere, and crosses the y-axis at - 1.
5.The point ![]() , rounded to
, rounded to ![]() for graphing purposes, is located on the graph of
for graphing purposes, is located on the graph of ![]() . The point
. The point ![]() , rounded to
, rounded to ![]() for graphing purposes, is located on the graph of
for graphing purposes, is located on the graph of ![]() .
.
Note that both points have the same x-coordinate and the y-coordinate's differ by a minus sign.
6.Mentally fold the coordinate system at the x-axis. Note that
when you fold the coordinate system at the x-axis, the graph
above the x-axis, ![]() , is superimposed on the graph below the x-axis,
, is superimposed on the graph below the x-axis, ![]() . This means both graphs are symmetric to each other with respect
to the x-axis.
. This means both graphs are symmetric to each other with respect
to the x-axis.
What exactly does that mean? Well for one thing, it means if
there is a point (a, b) on the graph of ![]() , we know that the point
(a, - b) is located on the graph of
, we know that the point
(a, - b) is located on the graph of ![]() . The vertical distance
between the two points is 2b.
. The vertical distance
between the two points is 2b.
7.The shapes are the same. The graph of ![]() is a reflection over the x-axis of the graph of
is a reflection over the x-axis of the graph of ![]() .
.
Mentally fold the graph of ![]() over the x-axis so that it is superimposed on the graph of
over the x-axis so that it is superimposed on the graph of ![]() . Every point on the graph of
. Every point on the graph of ![]() would be shifted down twice it's distance from the x-axis. For example, the point (a, 8) is located 8 units up from the x-axis. If we shifted
the point (a, 8) down 16 units, it would wind up at (a,- 8), 8 units below the x-axis.
would be shifted down twice it's distance from the x-axis. For example, the point (a, 8) is located 8 units up from the x-axis. If we shifted
the point (a, 8) down 16 units, it would wind up at (a,- 8), 8 units below the x-axis.
If the point (b, 11) is located on the graph of ![]() , it would
be shifted down 22 units to (b, -11) when the graph is reflected over the x-axis.
, it would
be shifted down 22 units to (b, -11) when the graph is reflected over the x-axis.
8.The point (0, 1) on the graph of ![]() would wind up at (0, -
1) after the graph was reflected over the x-axis.
would wind up at (0, -
1) after the graph was reflected over the x-axis.
9.Since ![]() , substitute f(x) for
, substitute f(x) for ![]() in the
equation
in the
equation ![]() to have g(x)=-f(x). This
means that for every value of x, the function values will differ
by a minus sign.
to have g(x)=-f(x). This
means that for every value of x, the function values will differ
by a minus sign.
If you would like to review any of the following, click on Example:
Reflection over the y-axis: The graph of f(x) versus the graph of f(-x)Example.
Vertical shifts: The graph of f(x) versus the graph of f(x) + C Example.
Horizontal shifts: The graph of f(x) versus the graph of f(x + C)Example.
Combination horizontal shift and reflection across the y-axis: The graph of f(x) versus the graph of f(- x + C) or f(C - x) Example.
Combination horizontal and vertical shifts: The graph of f(x) versus the graph of f(x + A) + B Example.
Combination horizontal and vertical shifts and reflections: The graph of f(x) versus the graphs of -f(x) + C. f(-x) + C, f(x + C) + D Example.
Stretch and Shrink: The graph of f(x) versus the graph of C(x) Example.
Stretch and Shrink: The graph of f(x) versus the graph of f(Cx) Example.
Combination of stretch, shrink, reflection, horizontal, and vertical shifts: Example.
Solving an equation from a graph: Example.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Nancy Marcus