

ON INVERSE FUNCTIONS
With Domain Restrictions

You can always find the inverse of a one-to-one function without restricting the domain of the function. Recall that a function is a rule that links an element in the domain to just one number in the range. You could have points (3, 7), (8, 7) and (14,7) on the graph of a function. A one-to-one function adds the requirement that each element in the range is linked to just one number in the domain. In this case, the above three points would not be points on the graph of a one-to-one function because 7 links to different numbers in the domain.
You can identify a one-to-one function from its graph by using the Horizontal Line Test. Mentally scan the graph with a horizontal line; if the line intersects the graph in more than one place, it is not the graph of a one-to-one function. If the function is not one-to-one, then its inverse will not be unique, and the inverse function must be unique. The domain of the original function must be restricted so that its inverse will be unique.
This section will show you how to restrict the domain and then find a unique inverse on that domain. Study the graph of a function that is not one-to-one and choose a part of the graph that is one-to-one. We will find the inverse for just that part of the graph.
The following is an example of finding the inverse of a function that is not one-to-one.
Problem 2: Find the inverse of the function ![]() .
.
Solution:
|
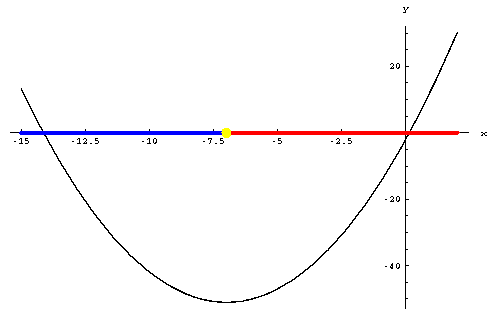
You could have also discovered the x = -7 dividing point by finding the vertex of the parabola. You can find the vertex of parabola by rewriting the original equation ![]() so that we have
so that we have ![]() . From the last form, we can read the vertex as (-7, -51). We are only interested in the x-part of the point, the -7.
. From the last form, we can read the vertex as (-7, -51). We are only interested in the x-part of the point, the -7.
![]()
![]()
![]()
![]()
![]()
![]()
Check:
Suppose you restricted the domain to ![]() . Choose a number from this domain, say -25. The function f takes the -25 to 973 because
. Choose a number from this domain, say -25. The function f takes the -25 to 973 because ![]() . The inverse function takes the 973 back to the -25 because
. The inverse function takes the 973 back to the -25 because ![]()
Review another problem concerning of finding the inverse of a function where the domain of the original function needs to be restricted.

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author:Nancy Marcus