ON INVERSE FUNCTIONS
Composition of Functions
Suppose the rule of function f(x) is 
and the rule of function g(x) is 
. Suppose now that you want to "leapfrog" the functions as follows: Take a 2 in the domain of f and link it to 9 with the f(x) rule, and then take the 9 and link it to 157 with the g(x) rule. This is a lot of work and you would rather just work with one function, a function that would link the 2 directly to the 157.
Since the g function operates on f(x), we can write the composition as g(f(x)). Let’s call the new function h(x) = g(f(x)). You can simplify from the inside out or the outside in.
Inside Out: 
Let’s check to see if the above function will link 2 directly to 157.
It
does.
Outside In: 
You can see that it is the same as the function we derived from the inside out.
The following is an example of finding the composition of two functions.
Example 2: Find 
and 
if 
and 
.
Comments:
. You can see that there is no graph to the left of the line x = 5. The graph only exists for x values located in the interval 
. This means that the domain of the composite function is the set of real numbers in the interval 
. Can you see the same thing without a graph?
The values of g(x), the set of real numbers in the interval 
, constitute the domain of the function f(g(x)). However; the values of g(x) only exist for the values of x in the domain of g(x) that belong to the set . The domain of the function equals the set of real numbers common to the sets and . Therefore, the domain of equals the set of real numbers in the set .
If you graph the function , you can see that the graph exists for values of x greater than a number between 7 and 8, and the graph exists for values of x less than a number between 0 and -1. Since 
, you can see that the expression 
must be equal to or greater than zero. This will happen when x belong to either the set of real numbers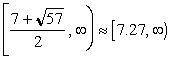 
or the set of real numbers number 
.
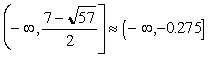If you are a bit rusty with your inequalities,
go to our Inequalities section for a review.
Therefore the domain of the composition function is the union of the above two sets.
Solution - :
Inside Out:
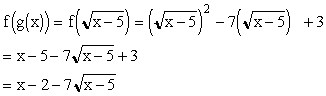
The composition function is equal to 
Outside In:
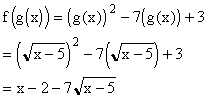
Check:
and the function f(x) links the 1 to the number -3 because 
.
Let’s see if the new function, let’s call it h(x), will link the 6 directly to the -3. 
It does and the new composition function can be written
Solution - 
:
Inside Out:
The composition function is equal to 
Outside In:
Check:
and the function g(x) links the 33 to the number 
because 
.
Let’s see if the new function, let’s call it h(x), will link the 10 directly to the .
It does and the new composition function can be written
Beginning students often ask why are these function different. They assume that the new function created by f(g(x)) is the same function as the one created by g(f(x)).
Wrong Assumption! Sometimes they are equal. Most of the time, these functions are different.
Review another example of finding the composition of functions.
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author:Nancy Marcus