

Find the solutions of the inequality
Start by moving the term on the right to the left:
Combine the terms on the left and simplify:
By now the inequality looks like
By using the quadratic formula, we find that the equation x2-x-4=0 has as its roots
The denominator is zero at 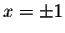 and x=-3.
and x=-3.
The solutions are all points in the set

[Back]
[Exercises]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Helmut Knaust
1998-06-16
Copyright © 1999-2024 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour



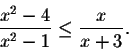
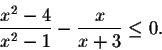
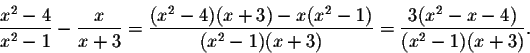
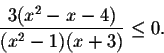
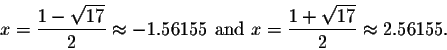
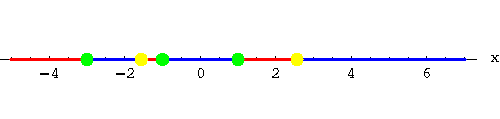
![\begin{displaymath}(-\infty,-3)\cup \left[\frac{1-\sqrt{17}}{2},-1\right)\cup \left(1,\frac{1+\sqrt{17}}{2}\right].\end{displaymath}](img40.gif)

 S.O.S MATHematics home page
S.O.S MATHematics home page 