Check that z=3 is a root of the resolvent cubic for the equation, then find all roots of the quartic equation.
First, we move the x-term to the right side:
Luckily, the left side is already a perfect square, so our equation looks like
Since
adding the terms 
on both sides yields
The right side is a quadratic polynomial in x:
It will become a perfect square when its discriminant is 0. This means we want to find z so that
The cubic polynomial
is the cubic resolvent; it is easy to check that z=3 is indeed a root of the cubic resolvent. Using the value z=3 in Equation (1), we obtain:
The right side is a perfect square:
Next, we take square roots, discarding one of the choices:
This quadratic equation has the complex roots
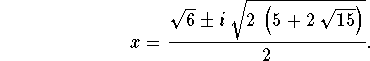
If we regard, on the other hand, the second choice of sign, we obtain the quadratic equation
This quadratic equation has the real roots
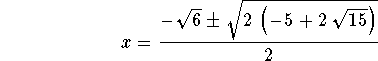
(Alternatively, 2 more roots can be found by polynomial long division.)
Thus the quartic equation
has the four roots:
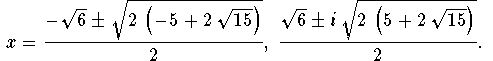
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Helmut Knaust