Show the following: If a polynomial has integer coefficients and its leading coefficient is 1, then all of its rational zeros are in fact integers.
By the Rational Zero Test, a rational zero of the form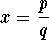 
must satisfy that q divides the leading coefficient 1; consequently 
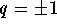, so 
an integer.
[Back]
[Exercises]
[Next]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Helmut Knaust
Tue Jun 24 12:51:02 MDT 1997
Copyright © 1999-2023 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour